DCGAN

Radford, Alec, Luke Metz, and Soumith Chintala. “Unsupervised representation learning with deep convolutional generative adversarial networks.” arXiv preprint arXiv:1511.06434 (2015).

The following is my reading notes of this paper.

1 Introduction

In this paper, they propose that one way to build image representations is by training GANs1, and later reusing parts of the generator and discriminator networks as feature extractors for supervised tasks.

GANs have been known to be unstable to train, often resulting in generators that produce nonsensical outputs.

Authors’ contributions:

  • They propose and evaluate a set of constraints on the architectural topology of Convolutional GANs that make them stable to train in most settings. They name this class of architectures Deep Convolutional GANs (DCGAN).
  • They use the trained discriminators for image classification tasks, showing competitive performance with other unsupervised algorithms.
  • They visualize the filters learnt by GANs and empirically show that specific filters have learned to draw specific objects.
  • They show that the generators have interesting vector arithmetic properties allowing for easy manipulation of many semantic qualities of generated samples.

2.1 Representation Learning from unlabeled data

  • do clustering on the data (e.g. K-means)2
  • train auto-encoders
    • stacked denoising autoencoders3
    • stacked what-where autoencoders4
    • ladder structures5
  • DBN6

2.2 Generating natural images

2.3 Visualizing the internals of CNNs

3 Approach and Model Architecture

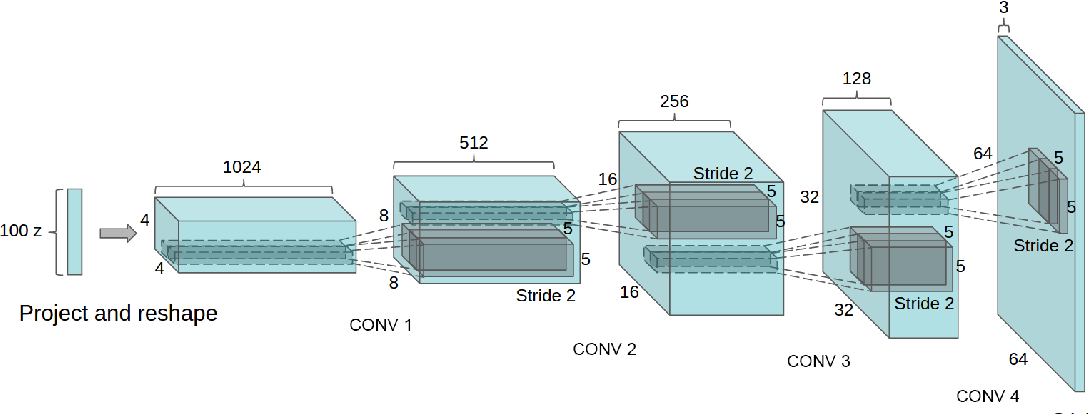
Figure 1: DCGAN generator used for LSUN scene modeling. A 100 dimensional uniform distribution Z is projected to a small spatial extent convolutional representation with many feature maps. A series of four fractionally-strided convolutions (in some recent papers, these are wrongly called deconvolutions) then convert this high level representation into a 64 × 64 pixel image. Notably, no fully connected or pooling layers are used.

Summary - architecture guidelines for stable DCGANs:

  • Replace any pooling layers with strided convolutions7 (discriminator) and fractional-strided convolutions (generator). This makes the model to learn its own upsampling/downsampling.
  • Use Batch Normalization8 in both the generator and the discriminator. BN stabilizes learning by normalizing the input to each unit to have zero mean and unit variance and help gradient flow in deeper models. To avoid sample oscillation and model instability, do not apply BN to the generator output layer and the discriminator input layer.
  • Remove fully connected hidden layers for deeper architectures. Global average pooling9 increased model stability but hurt convergence speed.
  • Use ReLU activation in generator for all layers except for the output, which uses Tanh. Using a bounded activation allows the model learn more quickly to saturate and cover the color space of the training distribution.
  • Use LeakyReLU activation in the discriminator for all layers, in contrast to the maxout activation which is used in the original GAN.

4 Details of adversarial training

  • Datasets:
    • Large-scale Scene Understanding (LSUN)10
    • Imagenet-1k
    • a newly assembled Faces dataset
  • No pre-processing was applied to training images besides scaling to the range of the tanh activation function $[-1, 1]$.
  • All models were trained with mini-batch SGD with mini-batch size of $128$.
  • All weights were initialized from Normal distribution $\mathcal{N}(0, 0.02)$.
  • In the LeakyReLU, the slope of the leak was set to $0.2$ in all models.
  • Use Adam optimizer11 with tuned hyperparameters.
  • Learning rate is $0.0002$ ($0.001$ is too high).
  • Reduce the momentum term $\beta_{1}$ from the suggested value $0.9$ to $0.5$ which helped stabilizing training.

4.1 LSUN

By showing samples from one epoch of training, in addition to samples after convergence, they demonstrate that the model is not producing high quality samples via simply overfitting/memorizing training examples.

4.1.1 Deduplication

4.2 Faces

4.3 Imagenet-1k

5 Empirical Validation of DCGANs capabilities

5.1 Classifying CIFAR-10 using GANs as a feature extractor

To evaluate the quality of the representations learned by DCGANs for supervised tasks, they train the model on Imagenet-1k and test it on CIFAR-10 (flatten and concatenate the features, then train a regularized linear L2-SVM classifier on top of them), achieving a good result.

5.2 Classifying SVHN digits using GANs as a feature extractor

Following preparation as in the CIFAR-10 experiments, they achieve SOTA test error on the SVHN dataset. Additionally, they train a purely supervised CNN with the same architecture on the same data and get a much worse result, which demonstrates that the CNN architecture in DCGAN is not the key contributing factor.

6 Investing and visualizing the internals of the networks

6.1 Walking in the latent space

Figure 4: Top rows: Interpolation between a series of 9 random points in Z show that the space learned has smooth transitions, with every image in the space plausibly looking like a bedroom. In the 6th row, you see a room without a window slowly transforming into a room with a giant window. In the 10th row, you see what appears to be a TV slowly being transformed into a window.

6.2 Visualizing the Discriminator Features

Figure 5: On the right, guided backpropagation visualizations of maximal axis-aligned responses for the first 6 learned convolutional features from the last convolution layer in the discriminator. Notice a significant minority of features respond to beds - the central object in the LSUN bedrooms dataset. On the left is a random filter baseline. Comparing to the previous responses there is little to no discrimination and random structure.

6.3 Manipulating the Generator Representation

6.3.1 Forgetting to draw certain objects

Figure 6: Top row: un-modified samples from model. Bottom row: the same samples generated with dropping out ”window” filters. Some windows are removed, others are transformed into objects with similar visual appearance such as doors and mirrors. Although visual quality decreased, overall scene composition stayed similar, suggesting the generator has done a good job disentangling scene representation from object representation. Extended experiments could be done to remove other objects from the image and modify the objects the generator draws.

6.3.2 Vector arithmetic on face samples

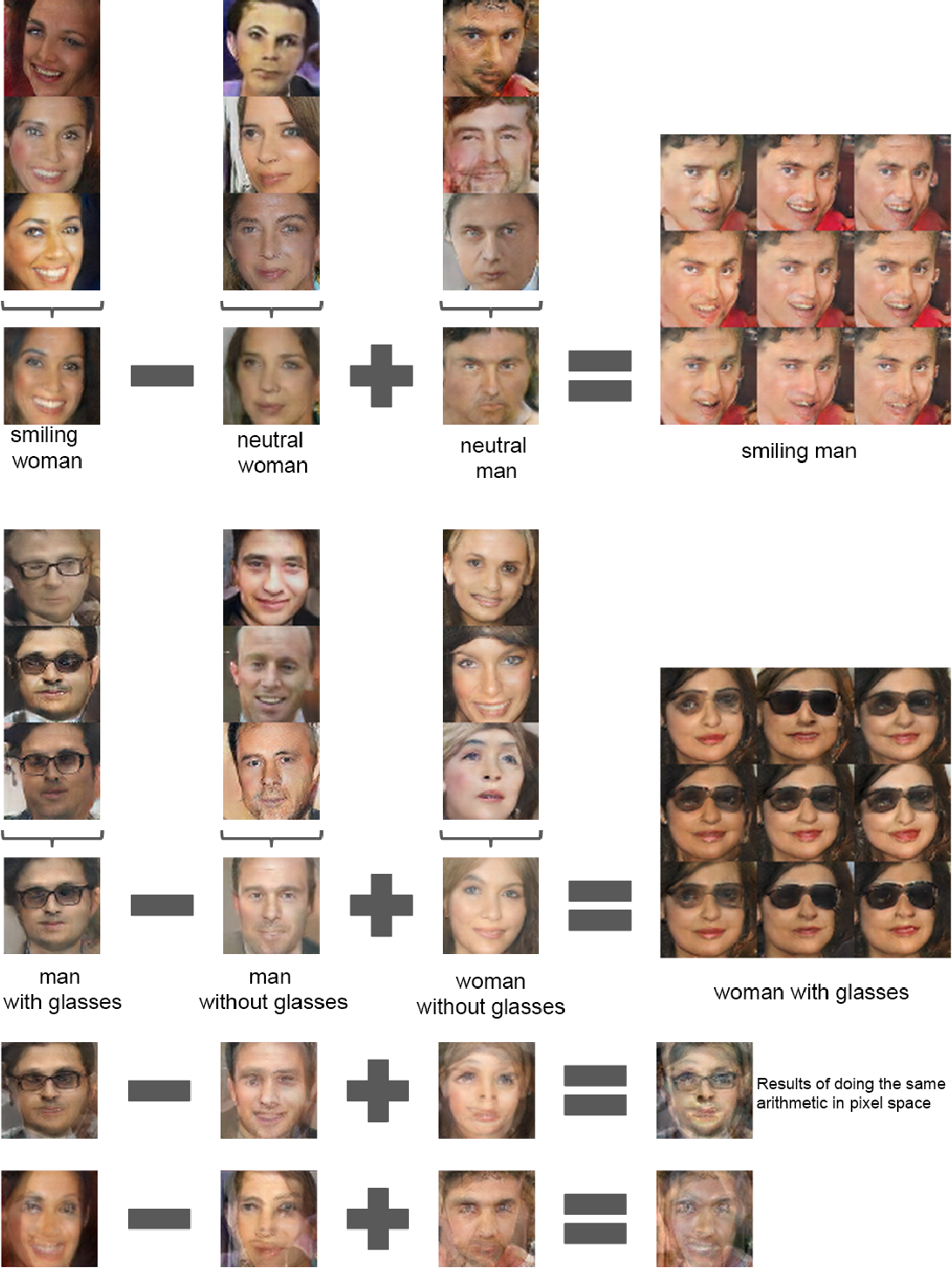
Figure 7: Vector arithmetic for visual concepts. For each column, the Z vectors of samples are averaged. Arithmetic was then performed on the mean vectors creating a new vector Y . The center sample on the right hand side is produce by feeding Y as input to the generator. To demonstrate the interpolation capabilities of the generator, uniform noise sampled with scale +-0.25 was added to Y to produce the 8 other samples. Applying arithmetic in the input space (bottom two examples) results in noisy overlap due to misalignment.

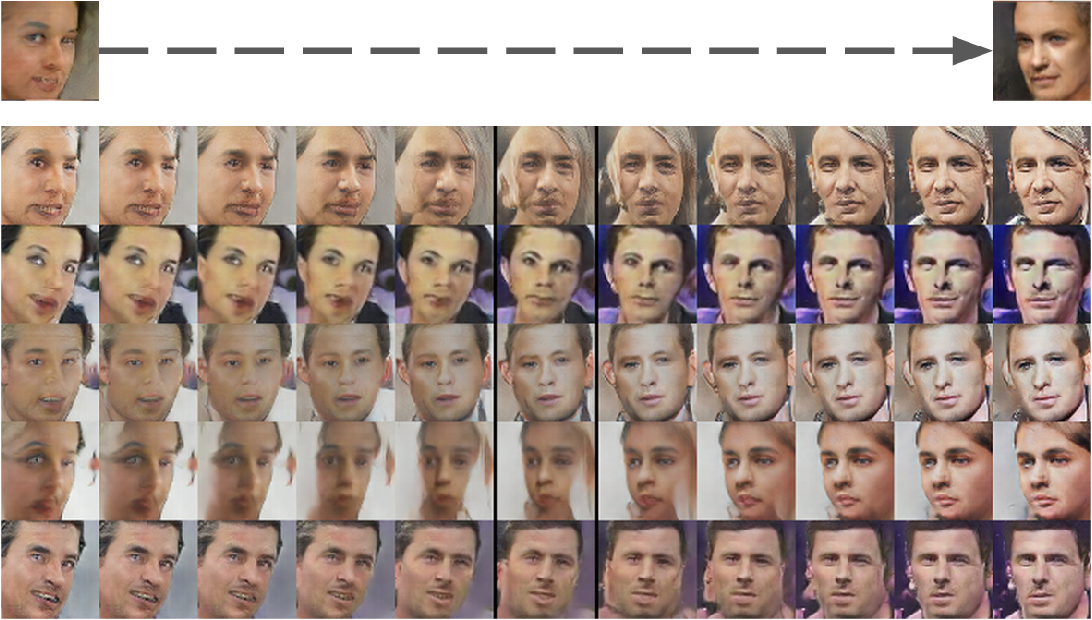
Figure 8: A ”turn” vector was created from four averaged samples of faces looking left vs looking right. By adding interpolations along this axis to random samples we were able to reliably transform their pose.

7 Conclusion and Future Work

“We propose a more stable set of architectures for training generative adversarial networks and we give evidence that adversarial networks learn good representations of images for supervised learning and generative modeling.”

Remaining forms of model instability - as model are trained longer they sometimes collapse a subset of filters to a single oscillating mode.

  1. Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in neural information processing systems. 2014. ↩

  2. Coates, Adam, and Andrew Y. Ng. “Learning feature representations with k-means.” Neural networks: Tricks of the trade. Springer, Berlin, Heidelberg, 2012. 561-580. ↩

  3. Vincent, Pascal, et al. “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion.” Journal of machine learning research 11.Dec (2010): 3371-3408. ↩

  4. Zhao, Junbo, et al. “Stacked what-where auto-encoders.” arXiv preprint arXiv:1506.02351 (2015). ↩

  5. Rasmus, Antti, et al. “Semi-supervised learning with ladder networks.” Advances in neural information processing systems. 2015. ↩

  6. Lee, Honglak, et al. “Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations.” Proceedings of the 26th annual international conference on machine learning. ACM, 2009. ↩

  7. Springenberg, Jost Tobias, et al. “Striving for simplicity: The all convolutional net.” arXiv preprint arXiv:1412.6806 (2014). ↩

  8. Ioffe, Sergey, and Christian Szegedy. “Batch normalization: Accelerating deep network training by reducing internal covariate shift.” arXiv preprint arXiv:1502.03167 (2015). ↩

  9. Inceptionism: Going Deeper into Neural Networks ↩

  10. Yu, Fisher, et al. “Lsun: Construction of a large-scale image dataset using deep learning with humans in the loop.” arXiv preprint arXiv:1506.03365 (2015). ↩

  11. Kingma, Diederik P., and Jimmy Ba. “Adam: A method for stochastic optimization.” arXiv preprint arXiv:1412.6980 (2014). ↩

Written on November 19, 2019